Theorem 2: An ordered Gibbs sampler applied to a consistent dependency network for
Theorem 2: An ordered Gibbs sampler applied to a
consistent dependency network for ![]() , where each
, where each ![]() is finite
(and hence discrete) and each local distribution
is finite
(and hence discrete) and each local distribution
![]() is
positive, defines a Markov chain with a unique stationary joint
distribution for
is
positive, defines a Markov chain with a unique stationary joint
distribution for ![]() equal to
equal to ![]() that can be reached from any
initial state of the chain.
that can be reached from any
initial state of the chain.
Proof: Let ![]() be the sample of
be the sample of ![]() after the
after the
![]() iteration of the ordered Gibbs sampler. The sequence
iteration of the ordered Gibbs sampler. The sequence
![]() can be viewed as samples drawn from a homogenous
Markov chain with transition matrix
can be viewed as samples drawn from a homogenous
Markov chain with transition matrix ![]() having elements
having elements
![]() . The matrix
. The matrix ![]() is the product
is the product
![]() , where
, where ![]() is the ``local''
transition matrix describing the resampling of
is the ``local''
transition matrix describing the resampling of ![]() according to the
local distribution
according to the
local distribution
![]() . The positivity of local
distributions guarantees the positivity of
. The positivity of local
distributions guarantees the positivity of ![]() , which in turn
guarantees the irreducibility of the Markov chain. Consequently,
there exists a unique joint distribution that is stationary with
respect to
, which in turn
guarantees the irreducibility of the Markov chain. Consequently,
there exists a unique joint distribution that is stationary with
respect to ![]() . The positivity of
. The positivity of ![]() also guarantees that this
stationary distribution can be reached from any starting point. That
this stationary distribution is equal to
also guarantees that this
stationary distribution can be reached from any starting point. That
this stationary distribution is equal to ![]() is proved in the
Appendix.
is proved in the
Appendix. ![]()
After a sufficient number of iterations, the samples in the
chain will be drawn from the stationary distribution for ![]() . We
use these samples to estimate
. We
use these samples to estimate ![]() . There is much written about
how long to run the chain before keeping samples (the ``burn in'') and
how many samples to use to obtain a good estimate (e.g., Gilks,
Richardson, and Spiegelhalter, 1996). We do not discuss
the details here.
Next, let us consider the use of Gibbs sampling to compute
. There is much written about
how long to run the chain before keeping samples (the ``burn in'') and
how many samples to use to obtain a good estimate (e.g., Gilks,
Richardson, and Spiegelhalter, 1996). We do not discuss
the details here.
Next, let us consider the use of Gibbs sampling to compute
![]() for particular instances
for particular instances ![]() and
and ![]() where
where ![]() and
and
![]() are arbitrary disjoint subsets of
are arbitrary disjoint subsets of ![]() . A naive approach uses
an ordered Gibbs sampler directly. During the iterations, only
samples of
. A naive approach uses
an ordered Gibbs sampler directly. During the iterations, only
samples of ![]() where
where
![]() are used to compute the conditional
probability. An important difficulty with this approach is that if
either
are used to compute the conditional
probability. An important difficulty with this approach is that if
either
![]() or
or ![]() is small (a common occurrence when
is small (a common occurrence when
![]() or
or ![]() contain many variables), many iterations are required
for an accurate probability estimate.
A well-known approach for estimating
contain many variables), many iterations are required
for an accurate probability estimate.
A well-known approach for estimating
![]() when
when ![]() is
small is to fix
is
small is to fix
![]() during ordered Gibbs sampling. It is not
difficult to generalize the proof of Theorem 2 to show that this
modified ordered Gibbs sampler has a stationary distribution and
yields the correct conditional probability given a consistent
dependency network.
When
during ordered Gibbs sampling. It is not
difficult to generalize the proof of Theorem 2 to show that this
modified ordered Gibbs sampler has a stationary distribution and
yields the correct conditional probability given a consistent
dependency network.
When ![]() is rare because
is rare because ![]() contains many variables, we can use
the independencies encoded in a dependency network along with
the law of total probability to decompose the inference task into a
set of inference tasks on single variables. For example, consider the
dependency network
contains many variables, we can use
the independencies encoded in a dependency network along with
the law of total probability to decompose the inference task into a
set of inference tasks on single variables. For example, consider the
dependency network
![]() . Given the independencies specified by this network,
we have
. Given the independencies specified by this network,
we have
Algorithm 1:
1 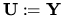 (* the unprocessed variables *)
(* the unprocessed variables *)
2 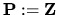 (* the processed and conditioning variables *)
(* the processed and conditioning variables *)
3 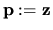 (* the values for
(* the values for 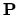 *)
*)
4 While 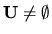
5 Choose 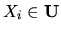 such that
such that 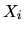 has no more parents in
has no more parents in 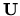 than any variable in
than any variable in 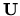
6 If all the parents of 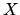 are in
are in 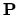
7 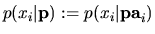
8 Else
9 Use a modified ordered Gibbs sampler to determine 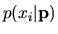
10 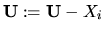
11 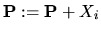
12 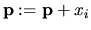
13 Return the product of the conditionals 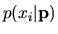
The key step in this algorithm is step 7, which bypasses
Gibbs sampling when it is not needed. This step is justified by
Equation 1.